Л.Э.ГЕНДЕНШТЕЙН,
ИСМО, г. Москва
Каковы «задачи задач» в школьном курсе физики?
Физика – один из немногих «задачных» школьных предметов: таковыми являются ещё только математика и химия. И именно эти предметы, причём именно из-за задач, являются обычно самыми трудными для учеников, а физика занимает, наверное, «почётное» первое место. Так стоят ли они, эти задачи, тех трудностей, из-за которых многие ученики отворачиваются (навсегда!) от нашего предмета? Что именно в задачах рождает негативное отношение к ним? Ведь сами по себе трудности могут даже привлекать (всем, к счастью, знакомы ребята, с увлечением «терзающие» трудные задачки)! Можно ли и нужно ли облегчать эти трудности?
Для ответа на эти важные вопросы надо поставить главный вопрос: каковы «задачи задач» в школьном курсе физики, т.е. какие цели они преследуют и удаётся ли этих целей добиться?
Трудность «задачных» предметов по сравнению с «незадачными» (историей, географией, биологией и пр.) обусловлена тем, что в «незадачных» предметах проверка знаний сводится большей частью к ответам на «репродуктивные» вопросы, т.е. к повторению фрагментов учебника или конспекта. По существу, это проверка памяти, а память у детей хорошая. А вот при решении задач (и только при решении задач!) проверяются понимание и умения. Формирование того и другого требует внутренней работы, – но она не только трудна, а и приносит радость, – более того, только эта внутренняя работа и приносит радость при учёбе! И только от неё и есть настоящая польза от учения.
Мы намеренно разделили здесь понимание и умения, хотя они, конечно, взаимосвязаны. Понимание при изучении физики как школьного предмета относится преимущественно к самой физике: это понимание физических закономерностей, взаимосвязей между физическими явлениями и т.д. Формированию понимания в наибольшей степени способствуют не расчётные задачи, а качественные и устные или полуустные задачи-одноходовки.
Например: «Как изменятся давление и сила давления человека на пол, если он поднимет одну ногу?» или «Какие превращения энергии происходят при движении камня, брошенного вверх, без учёта сопротивления воздуха? с учётом сопротивления воздуха?» Такими задачами желательно завершать изложение разделов теории и даже включать их в изложение. Подобные задачи хорошо принимаются учениками, могут служить темой обсуждений всем классом. И они действительно позволяют понять суть изучаемых явлений и их взаимосвязь.
Умения же при изучении физики как школьного предмета относятся в основном к общеучебным умениям, главным образом – к построению и анализу математических моделей явлений и процессов.
По существу, физика – единственный школьный предмет, в котором мы на протяжении нескольких лет учим ребят строить математические модели.
В этом смысле расчётные задачи по физике являются преемниками так называемых «текстовых» задач в курсе математики (на движение, совместное действие и т.п.), которые и там часто являются наиболее трудными. Поэтому неудивительно, что школьный курс физики «наследует» эти трудности и приумножает их, поскольку в ходе изучения физики значительно расширяется круг моделируемых ситуаций.
Так что, как видим, избегать этих трудностей при изучении физики – значит в значительной степени выхолащивать одну из важнейших целей школьного курса физики. Но действительно ли эти цели достигаются? И можно ли избежать отрицательного эффекта этих трудностей?
Для ответа на этот вопрос надо понять, что именно вызывает у учеников неприятие задач. Сами ученики говорят, что:
• они часто забывают значения букв, обозначающих физические величины;
• они забывают сами формулы;
• решать задачи им не интересно.
Нам кажется, что всё это является следствием главного недостатка в подборе и методике задач традиционного школьного курса. Он проявляется в том, что построение математической модели лишено смысла в глазах ученика: он не видит другой цели в решении задачи, кроме той убогой, чтобы после подстановки численных значений величин в формулу, полученную при решении задачи в «общем виде», ответ совпал бы с ответом в конце учебника или задачника. Что и говорить, «великая цель»! Странно было бы, если бы у кого-то такая цель вызывала энтузиазм.
На самом же деле ценность математической модели состоит не только и не столько в её построении, сколько в её анализе, т.е. как раз в том, что остаётся обычно «за бортом» при решении задач в школе! Рассмотрим это подробнее.
На наш взгляд, ценность расчётных задач по физике состоит в:
• построении математической модели, т.е. умении увидеть наиболее существенные для данной задачи особенности описанной словесно ситуации, записи в математическом виде основных физических закономерностей («формул»), связывающих данные и искомые величины;
• работе с математической моделью, проявляющейся в умении оперировать математическими выражениями (очень простыми в школьном курсе!), т.е. в составлении и решении уравнений;
• анализе результатов математической модели, т.е. качественном выявлении предсказываемых моделью закономерностей, что требует некоторого навыка работы с формулами (в процессе работы этот навык и вырабатывается). При этом выясняется взаимозависимость физических величин, соответствие или, что особо ценно, несоответствие следствий из полученного «в общем виде» решения ожиданиям, выяснению возможных причин такого несоответствия;
• оценке полученного численного результата с точки зрения его «разумности», выявление возможных причин «неразумности».
Для того, чтобы можно было реализовать весь этот богатый арсенал, необходим тщательный подбор задач и продуманная методика работы с ними. Особое внимание следует уделить осмысленности в глазах ученика всех этапов работы с задачами – только это может вызвать у него интерес к решению задач, и, как следствие, успехи и преобразование «отрицательного имиджа» задач в «положительный». Вот возможные методы и приёмы, подтвердившие себя в педагогической практике:
1. Задачи-сравнения. Численный ответ задачи сравнивается со значением известной ученику величины. Такое сравнение может вызвать удивление. Например: «Что больше – масса воздуха в вашей комнате или ваша масса?» Ответ поражает ученика: масса воздуха в комнате средних размеров сопоставима с массой взрослого человека!
2. Задачи с сюжетом. В этом случае от численного значения ответа «зависит чья-то судьба». Например, ягуар, самый быстрый зверь, замечает антилопу, находящуюся от него на заданном расстоянии, и начинает погоню. Антилопа бежит не так быстро, но зато может бежать долго, а ягуар со своей рекордной скоростью – не более одной минуты. Догонит ли ягуар антилопу за эту минуту?
3. Задачи с особенно неожиданным ответом. Например: «Как изменяется суммарная кинетическая энергия молекул в воздухе комнаты при включении отопления?» Простой расчёт на основе уравнения состояния газа показывает, что совершенно не изменяется! При повышении температуры увеличивается средняя кинетическая энергия молекул, но их число уменьшается в точности так, что суммарная кинетическая энергия молекул остаётся неизменной. Значит, отапливая помещение, мы, по существу, отапливаем «улицу»! Этот важный «экологический» вывод навсегда запомнится ученику.
4. Задачи для осознания особенно больших и малых величин. Например: «Что больше – число молекул в чайной ложке воды или число чайных ложек воды в Мировом океане?» Оказывается, это – величины одного порядка. При решении этой задачи «мобилизуется» широкий спектр простых, известных ученикам соотношений и есть простор для простых опытов. Оценить массу воды в чайной ложке можно, измерив, сколько ложечек нужно, чтобы наполнить стакан (для оценки достаточно половины стакана). А примерно оценить массу воды в Мировом океане можно, приняв, что средняя глубина океанов составляет несколько километров и они покрывают большую часть площади земного шара.
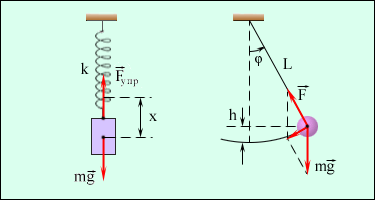
5. Качественный анализ полученной формулы. При этом ценность представляют, как очевидные подтверждения формулы (это дополнительная и очень ценная проверка её правильности), так и неочевидные выводы, позволяющие углубить представления о физических понятиях. Например, в задаче о двух грузах массами m1 и m2, висящих на нити, переброшенной через неподвижный блок, ответ для проекции ускорения грузов 
Отсюда видно, что: 1) если поменять грузы местами, проекция ускорения поменяет знак; 2) если массы грузов равны, ускорение равно нулю; 3) если одна из масс намного больше другой, ускорение по модулю приближается к ускорению свободного падения (на одном конце нити – гиря, а на другом – муха: гиря падает, «не замечая» мухи!). Неожиданный ответ – в сравнении весов грузов. Ускорение оказывается, как раз таково, что веса грузов равны, несмотря на отличие в их массах! Но причина понятна: ведь вес каждого из грузов – это сила, с которой он растягивает нить, а натяжение нити с двух сторон от блока одинаково (массой блока и трением в нём мы, конечно, в таких задачах пренебрегаем).
6. Задачи с неожиданно простым «устным» решением. Например, задача о пути, пройденном собакой, которая бегает между двумя мальчиками, идущими навстречу друг другу, – этот путь находится сразу, как только найдено время бега, т.е. время движения мальчиков до встречи (скорость собаки даётся в условии).
7. Задачи с «подвохом». Например: «Из двух городов, находящихся на расстоянии 200 км, навстречу друг другу выехали два автомобиля со скоростями соответственно 40 км/ч и 60 км/ч. Через какое время расстояние между автомобилями будет равно 100 км?» Первый ответ (1 ч) ученики находят легко. Второй возможный ответ – 3 ч (через 1 ч после встречи автомобилей) – почти никем сразу не обнаруживается, и его «открытие» вызывает порой бурные эмоции.
Наконец, желательно составлять задачи так, чтобы правильность полученных численных значений ученик мог оценить с помощью здравого смысла и житейского опыта, а не только сравнивая их с «правильными» в конце учебника или задачника. К сожалению, это очень редко выполняется в большинстве учебников и задачников. А «бесстрастный» ответ типа «8,3 Дж» или «3 10–3 мм» мало что скажет ученику.
И наконец о решении задач в «общем виде» и традиционной формуле записи решения («Дано», «Решение»), отделённой вертикальной чертой со всеми атрибутами. Во многих случаях то и другое, конечно, полезно, потому что позволяет организовать и систематизировать работу над задачами. Но порой эти требования становятся «прокрустовым ложем». Например, задачи на формулу линзы намного проще решаются «по действиям», а не в «общем виде», и тогда они доступны даже семикласснику. А многие задачи с «изюминкой» вообще не могут быть уложены в какую-то схему, но именно такие задачи наиболее ценны! К тому же традиционная форма записи предусматривает только один вид «анализа» – проверку размерности ответа. А для самого главного – анализа полученной формулы и оценке следствий из неё – места не предусмотрено. Учитывая к тому же, что роль тестов возрастает, а также то, что на олимпиадах и вступительных экзаменах форма записи решения практически не учитывается, вряд ли стоит так за неё «держаться».
Изложенные соображения и рекомендации позволят, на наш взгляд, значительно повысить роль задач в школьном курсе физики и преодолеть связанное с задачами отрицательное отношение учеников к нашему предмету.
Автор: Л.Э.ГЕНДЕНШТЕЙН