Лекция №15. Ассиметричные криптосистемы шифрования
Оглавление
Метод Диффи—Хелмана передачи секретного ключа по незащищенному каналу 3
Концепция асимметричного шифрования 5
Алгоритм асимметричного шифрования RSA 8
Введение
Симметричный подход к шифрованию изначально несет в себе очевидную проблему, называемую проблемой распределения ключей (key distribution), которая состоит в следующем. Отправитель и получатель хотят обмениваться секретными сообщениями, но в их распоряжении имеется незащищенный открытый канал. Поэтому они вынуждены использовать шифрование, но чтобы послать зашифрованное сообщение, нужно предварительно обменяться секретной информацией о значении ключа. Однако секретный ключ нельзя передать по открытому каналу. Если его зашифровать другим ключом, то опять возникает проблема доставки второго ключа. Получается замкнутый круг.
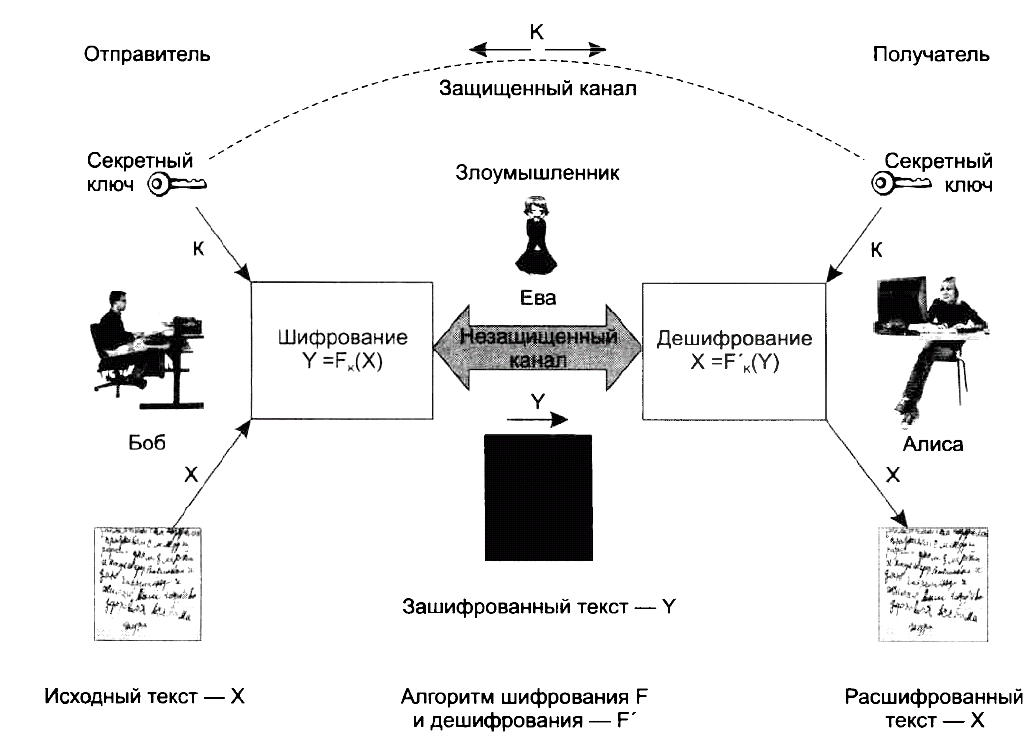
Рис. 1. Симметричное шифрование.
Единственным по-настоящему надежным решением этой проблемы является передача ключа при личной встрече абонентов. Однако при активном обмене требуется часто менять ключи, чтобы не дать возможности криптоаналитику собрать большое количество шифрованного материала, — известно, что чем больше зашифрованных сообщений окажется в руках криптоаналитика, тем легче ему раскрыть криптосистему.
Криптоаналитик — специалист по криптоанализу. Одним из первых криптоаналитиков был Аристотель, криптографически вскрывший скиталу — одно из первых известных криптографических устройств.
Современный криптоаналитик должен иметь познания в области математики и теории алгоритмов. Часто также является криптографом — специалистом по созданию и использованию средств шифрования.
Скитала (или сцитала — от греческого σκυτάλη, жезл) — инструмент, используемый для осуществления перестановочного шифрования, в криптографии известный также как шифр Древней Спарты. Представляет собой цилиндр и узкую полоску пергамента, на которой писалось сообщение, обматывавшуюся вокруг него по спирали. Античные греки и спартанцы, предположительно, использовали этот шифр для обмена сообщениями во время военных кампаний.

Рис. 2. Сцитала.
Криптоанализ (от др.-греч. κρυπτός — «скрытый» и «анализ») — наука о методах расшифровки зашифрованной информации без предназначенного для такой расшифровки ключа и сам процесс такой расшифровки. В большинстве случаев под криптоанализом понимается выяснение ключа; криптоанализ включает также методы выявления уязвимости криптографических алгоритмов или протоколов.
Кроме того, если злоумышленник перехватывает и сохраняет сообщения, зашифрованные одним и тем же ключом, то при раскрытии данного ключа они все окажутся скомпрометированными. Следовательно, необходимы частые личные встречи абонентов для обмена ключами, что, во-первых, не всегда возможно, а во-вторых, вообще делает бессмысленным обмен данными по каналу связи — действительно, зачем шифровать данные, если их можно лично передать при встрече.
Менее надежным способом распределения ключей является использование курьеров или других вариантов защищенной доставки ключей, но это решение тоже имеет очевидные изъяны. Существуют и другие приемы, не решающие, но смягчающие проблему распределения ключей. Например, у абонента может быть несколько секретных ключей, которые он должен использовать по разному назначению. Один ключ выдается ему на долгий срок, этот ключ применяется только для шифрования (дешифрования) других ключей — кратковременных, каждый из которых действителен только на время одного сеанса связи. И хотя в этом случае все равно остается проблема доставки долговременного ключа, уже нет необходимости его частой смены, так как этот ключ используется относительно редко и шифрует небольшие порции данных — сеансовые ключи.
Несмотря на различные усовершенствования процедуры распределения ключей, они не могут полностью устранить коренной изъян симметричных методов — необходимость доставки секретного ключа по незащищенному каналу.
Если проблема с ключами возникает в системе с двумя абонентами, то она многократно усугубляется в системе с большим числом абонентов. Пусть, например, n абонентов хотят обмениваться секретными данными по принципу «каждый с каждым», в этом случае потребуется n(n — 1)/2 ключей, которые должны быть сгенерированы и распределены надежным образом. То есть количество требуемых ключей пропорционально квадрату количества абонентов, что при большом числе абонентов делает задачу чрезвычайно сложной. Но именно такая ситуация наблюдается во всех современных сетях связи — телефонных, радио и компьютерных. Все это сделало чрезвычайно актуальной проблему распределения ключей.
Метод Диффи—Хелмана передачи секретного ключа по незащищенному каналу
В середине 70-х годов американские ученые Мартин Хеллман и Уилтфилд Диффи нашли способ, с помощью которого абоненты могли безопасно обмениваться секретными ключами без передачи их по каналу связи.

Рис. 3. Уилтфилд Диффи и Мартин Хеллман
Особенность этого открытия состоит в том, что оно противоречит всем интуитивным представлениям человека, делает возможным то, что кажется «очевидно» невозможным.
Метод Диффи—Хеллмана основан на использовании свойств односторонних функций.
Односторонняя функция (one-way function) — это функция у = F(х), которая легко вычисляется для любого входного значения х, но обратная задача — определение х по заданному значению функции у — решается очень трудно.
Примером односторонней функции может служить простейшая функция двух аргументов F(p, q) = pq, представляющая собой произведение двух простых чисел р и q, она вычисляется сравнительно просто, даже если числа р и q очень большие. Но чрезвычайно сложно решить обратную задачу (называемую факторизацией) — по произведению подобрать исходные два простых числа.
Другой пример — функция Y(x) = Dx mod Р, которая при некоторых ограничениях на параметры D и Р является односторонней, то есть, зная Y, а также параметры D и Р, нельзя без экстраординарных вычислительных усилий найти аргумент х.
Итак, пусть Алиса и Боб решили обмениваться шифрованными сообщениями, но в их распоряжении имеется только незащищенный открытый канал связи, при этом никаких возможностей встретиться или передать секретный ключ через кого-нибудь другого у них нет. В соответствии с алгоритмом Диффи—Хеллмана для успешного решения задачи Алиса и Боб должны выполнить следующие действия. Предварительно они открыто договариваются о том, что будут использовать одностороннюю функцию Y(x)=Dx mod Р. Затем они договариваются о значениях параметров D и Р.
Пусть, например, они договорились, что D = 7 и Р = 13, то есть функция имеет вид
Y(x) = 7х mod 13.
Еще раз подчеркнем, что в соответствии с алгоритмом Диффи—Хеллмана вся эта информация не является секретной, и даже если переговоры будут подслушаны Евой, это не даст ей возможности прочитать сообщения Алисы и Боба. Дальнейшие действия участников обмена описываются в табл. 1.
Таблица 1. Действия Алисы и Боба в соответствии с алгоритмом Диффи—Хеллмана

В результате описанной процедуры на шаге 4 Алиса и Боб получили одно и то же число 3! Математические преобразования показывают, что вычисления Алисы и Боба всегда будут давать одинаковые результаты. Полученные в результате числа они могут использовать в качестве известного только им ключа для различных симметричных методов шифрования.
Посмотрим, может ли Ева подобрать разделяемый секретный ключ Алисы и Боба. Пусть на шаге 3, когда Алиса и Боб посылали друг другу свои открытые ключи а(10) и b(9), Ева смогла перехватить эти числа (ведь канал является открытым) и теперь пытается вычислить разделяемый секретный ключ. Зная число a, которое Алиса послала Бобу, Ева хочет повторить действия Боба и вычислить разделяемый секретный ключ по формуле 10Bmod 13. Для этого ей требуется закрытый ключ Боба В, который он, однако, хранит секретно от всех. Зато Ева знает, что Боб использовал свой закрытый ключ В, когда вычислял значение своего открытого ключа — b.
То есть задача будет решена, если Ева сможет подобрать такое значение B, чтобы значение 7Вmod13 равнялось 9. Но именно это практически неразрешимо, поскольку функция 7Вmod13 является односторонней. Таким образом, Алиса и Боб действительно получили секретный ключ.
Для того чтобы усложнить решение обратной задачи, то есть восстановление закрытого ключа Алисы или Боба по открытому, на параметры алгоритма накладываются некоторые ограничения, в том числе следующие:
- все параметры D, Р, A, В должны быть целыми положительными числами;
- A и B должны быть большими числами порядка 10100;
- Р должно быть большим простым числом порядка 10300, причем желательно, чтобы (Р — 1)/2 также было простым числом;
- число D не обязательно должно быть большим, обычно оно выбирается меньше десяти, D<P.
Хотя алгоритм Диффи—Хеллмана стал прорывом в области криптографии, в его исходном состоянии он представлял скорее теоретическую, нежели практическую ценность. Устранив препятствие в виде необходимости надежного закрытого канала для передачи ключа, этот метод не снял проблемы квадратичной зависимости числа ключей от числа абонентов. Решение пришло очень скоро: уже через год после появления алгоритма Диффи—Хеллмана была теоретически доказана возможность принципиально нового подхода к шифрованию — асимметричного шифрования, при использовании которого (помимо прочих преимуществ) кардинально упрощается задача распределения ключей.
Концепция асимметричного шифрования
До сравнительно недавнего времени понятие «симметричное шифрование» не существовало просто потому, что все методы, которые использовались человечеством на протяжении нескольких тысяч лет, по современной классификации могли быть отнесены к классу симметричных, других просто не было. Более того, все эти тысячи лет существовала твердая убежденность, что в принципе никогда не может быть иных схем, кроме симметричной, когда отправитель шифрует с помощью секретного ключа, получатель с помощью этого же ключа расшифровывает!
Революция свершилась в конце 60-х — середине 70-х, когда с разницей в несколько лет две группы ученых, одна из которых — уже знакомые нам Диффи и Хеллман, а другая — сотрудники секретной правительственной лаборатории Великобритании Эллис, Кокс и Уильямсон, независимо друг от друга изобрели принципиально новый подход к шифрованию, открывающий глобальные перспективы в области современных коммуникаций.
Предельно упрощая, этот подход можно описать фразой: «отправитель шифрует сообщение с помощью одного ключа, а получатель расшифровывает его с помощью другого ключа». Как видим, здесь на двух сторонах обменного канала используются разные ключи, то есть присутствует асимметрия, соответственно все методы, основанные на таком подходе, стали называть «асимметричными».
Это удивительно, что за несколько тысяч лет не было ни одной известной науке попытки изобретения асимметричного метода шифрования, и вдруг, практически одновременно, две независимые группы ученых совершают это открытие! Возможно, причина кроется в том, что к концу 60-х годов совпало два обстоятельства: во-первых, возникла острая потребность в новом типе шифрования, во-вторых, появились технические возможности реализации этой идеи.
Потребность была продиктована зрелостью таких видов массовых коммуникаций, как телефон, радио, компьютерные сети, для которых, во-первых, особенно важна секретность ввиду слабой защищенности публичных средств связи, а во-вторых, неприемлемы ограничения традиционных методов шифрования, выражающиеся в необходимости обмена секретным ключом для каждой пары абонентов. К концу 60-х годов стали отчетливо вырисовываться перспективы использования Интернета как мировой сети связи, и одновременно с этим стало приходить осознание того, что глобальная публичная сеть может выполнить свою миссию только в том случае, если миллионам ее пользователей будет предоставлена возможность защищенного обмена сообщениями. Эти темы особенно волновали военных разных стран, которых очень привлекала возможность распределенного управления вооружёнными силами, но пугала невозможность гарантировать секретность передаваемых директив. И если в недалеком прошлом проблема распределения секретных ключей хотя и существовала, но была преодолимой, то в новых условиях она стала принципиальным препятствием.
К этому времени созрели технические возможности реализации вычислительно емких алгоритмов шифрования, к которым могут быть отнесены асимметричные алгоритмы. Массовое распространение получили компьютеры, обладающие такой вычислительной мощностью, которой до сих пор могли похвастаться только уникальные модели суперкомпьютеров. Это сделало шифрование обыденной операцией, которая может быть выполнена на обычном персональном компьютере.
Вот на таком историческом фоне была предложена концепция асимметричной криптосистемы, называемой также шифрованием с открытым ключом.
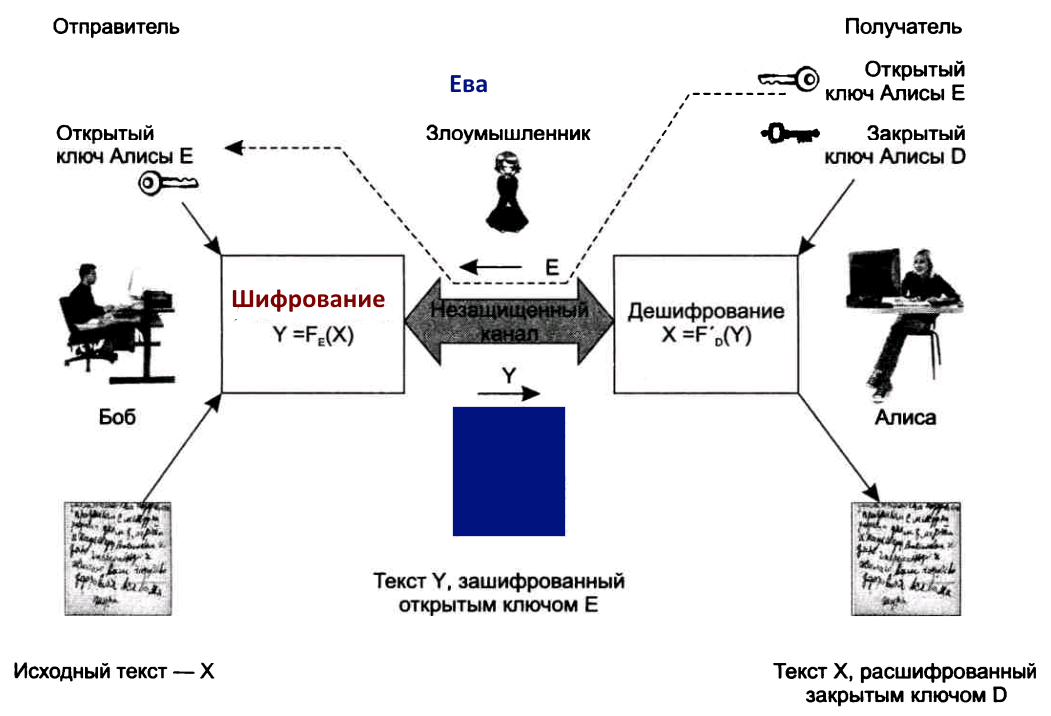
Рис. 4. Модель асимметричной криптосистемы.
Так же, как и в модели симметричного шифрования (см. рис. 1), здесь показаны три участника: отправитель (Боб), получатель (Алиса) и злоумышленник (Ева). В отличие от симметричной схемы шифрования, в которой наличие разделяемого секретного ключа автоматически означает возможность двустороннего защищенного обмена, здесь существует отдельная процедура для передачи зашифрованных сообщений в каждую из сторон. На рисунке показан вариант, когда зашифрованные сообщения могут быть посланы только Бобом в сторону Алисы, но не наоборот.
Итак, Алиса пожелала, чтобы Боб посылал ей зашифрованные сообщения. Для этого она сгенерировала пару ключей: открытый ключ (public key) Е и закрытый ключ (private key) D. Для шифрования текста служит открытый ключ, но расшифровать этот текст можно только с помощью закрытого ключа. Алиса не хочет, чтобы кто-либо читал ее почту, поэтому она сохраняет закрытый ключ D (часто называемый также личным ключом) в секрете. Открытый же ключ Е Алиса свободно передает всем, от кого хочет получать зашифрованные сообщения. Открытый ключ не представляет никакого секрета, Алиса может поместить его на своей странице в социальной сети или обнародовать в рекламе на телевидении. Все, кто хотят посылать Алисе зашифрованные сообщения, используют один и тот же ключ Е, но при этом никто из них не может прочитать сообщения друг друга.
1. Алиса передает Бобу свой открытый ключ Е по незащищенному каналу в незашифрованном виде.
2. Боб шифрует свое сообщение X открытым ключом Алисы Е и посылает зашифрованный текст Y = FE(X) по открытому каналу. Никто не может прочитать это сообщение. Даже сам Боб, если бы ему вдруг захотелось перечитать, что он там написал, не смог бы этого сделать, потому что для этого нужен закрытый ключ Алисы, которого у него нет.
3. Алиса получает шифрованное сообщение Y =FE(X) и расшифровывает его своим закрытым ключом D: X = F’D(Y).
Для того чтобы в сети все n абонентов имели возможность не только принимать зашифрованные сообщения, но и сами посылать таковые, каждый абонент должен обладать собственной парой ключей Е и D. Всего в сети будет 2n ключей: n открытых ключей для шифрования и n секретных ключей для дешифрования. Таким образом решается проблема масштабируемости: квадратичная зависимость количества ключей от числа абонентов в симметричных алгоритмах заменяется линейной зависимостью в асимметричных алгоритмах. Решается и проблема доставки ключа, поскольку теперь он не является секретом, его можно без опаски передавать по открытому каналу. Злоумышленнику нет смысла стремиться завладеть открытым ключом, поскольку это не дает возможности расшифровать текст или вычислить закрытый ключ.
Алгоритм асимметричного шифрования RSA
Открыватели асимметричного подхода к шифрованию показали концептуальную возможность существования функций, позволяющих построить криптографическую систему, в которой текст шифруется одним ключом, а расшифровывается — другим. Они также обрисовали те перспективы, которые открывает этот подход в деле решения проблемы распределения ключей. Ими были сформулированы два принципиальных требования, которым должны удовлетворять функции асимметричной криптосистемы:
- зашифрованное сообщение должно быть результатом вычислений односторонней функции, так чтобы никто не мог выполнить обратные преобразования и получить исходный текст;
- эта односторонняя функция должна быть сконструирована таким образом, чтобы у нее был некоторый секретный элемент, зная который получатель шифровки мог легко выполнить обратное преобразование.
 Функции, которые удовлетворяют данным требованиям, назвали односторонними функциями с потайным входом (trapdoor function). Некоторое время ученым не удавалось найти функции, удовлетворяющие этим критериям, поэтому идея асимметричного шифрования не находила практического применения. Наконец, в 1978 году трое американских ученых, Ривест, Шамир и Адлеман, предложили долгожданный алгоритм асимметричного шифрования RSA, названный так по первым буквам их фамилий — Rivest, Shamir, Adleman. В табл. 2 описываются основные шаги алгоритма RSA.
Функции, которые удовлетворяют данным требованиям, назвали односторонними функциями с потайным входом (trapdoor function). Некоторое время ученым не удавалось найти функции, удовлетворяющие этим критериям, поэтому идея асимметричного шифрования не находила практического применения. Наконец, в 1978 году трое американских ученых, Ривест, Шамир и Адлеман, предложили долгожданный алгоритм асимметричного шифрования RSA, названный так по первым буквам их фамилий — Rivest, Shamir, Adleman. В табл. 2 описываются основные шаги алгоритма RSA.
Таблица 2. Последовательность действий участников обмена данными в соответствии с алгоритмом RSA.
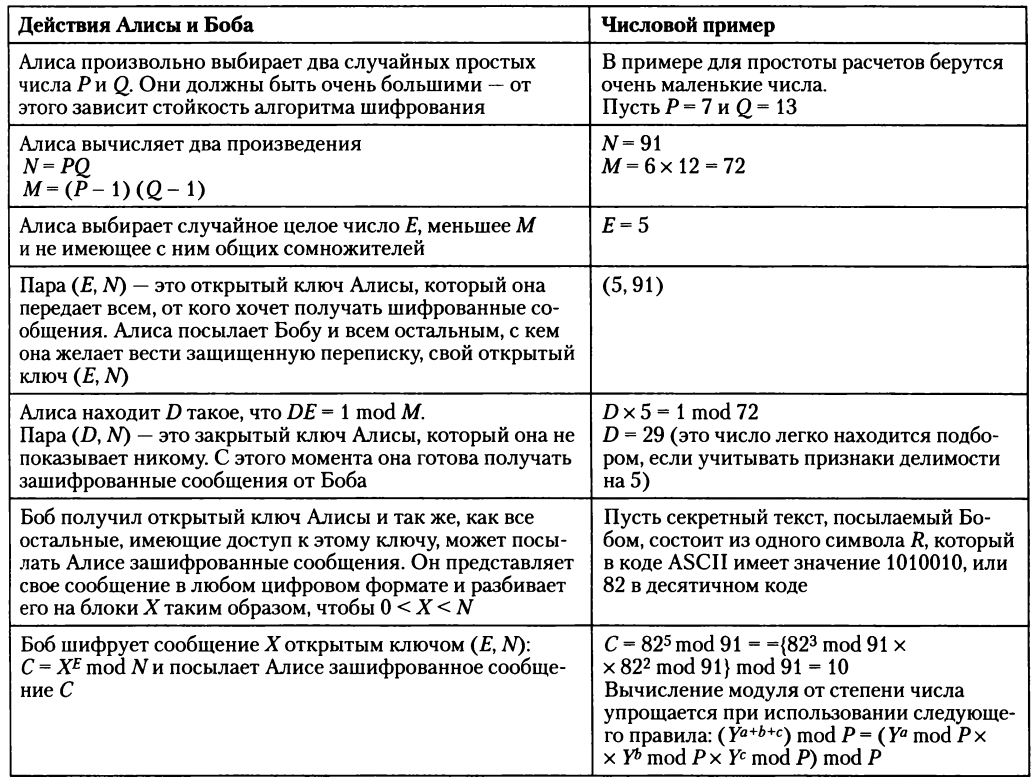

Еве для того, чтобы прочитать перехваченное сообщение С, требуется закрытый ключ Алисы (D, N). Но в ее распоряжении имеется только открытый ключ (E, N). Теоретически, зная открытый ключ, можно вычислить значение закрытого ключа. Однако необходимым промежуточным действием в этом преобразовании является нахождение простых чисел Р и Q, для чего нужно разложить на простые множители очень большое число N, а это является чрезвычайно трудоемкой процедурой. Таким образом, здесь мы имеем дело с односторонней функцией N= PQ. Но для Алисы это же действие — разложение большого числа на два простых множителя — не представляет никакого труда, потому что она знает, как сконструировано это число N, она сама его вычислила, произвольно выбрав два сомножителя. Другими словами, Алисе известен «потайной вход» этой односторонней функции. Именно с огромной вычислительной сложностью разложения большого числа N на простые множители Р и Q связана высокая криптостойкость алгоритма RSА.
Хотя информация об открытом ключе не является секретной, ее нужно защищать от подлогов, чтобы злоумышленник под именем легального пользователя не навязал свой открытый ключ, после чего с помощью своего закрытого ключа он мог бы расшифровывать все сообщения, посылаемые легальному пользователю, и отправлять свои сообщения от его имени. Решение проблемы дает технология цифровых сертификатов — электронных документов, которые связывают конкретных пользователей с конкретными открытыми ключами.