Лекция 14. Основные понятия криптографической защиты информации и виды криптосистем.
Введение.
Безопасность данных означает их конфиденциальность, целостность и подлинность. Критерии безопасности данных могут быть определены следующим образом.
Конфиденциальность данных предполагает их доступность только для тех лиц, которые имеют на это соответствующие полномочия.
Под обеспечением конфиденциальности информации понимается создание таких условий, при которых понять содержание передаваемых данных может только законный получатель, кому и предназначена данная информация.
Целостность информации предполагает ее неизменность в процессе передачи от отправителя к получателю. Под обеспечением целостности информации понимается достижение идентичности отправляемых и принимаемых данных.
Подлинность информации предполагает соответствие этой информации ее явному описанию и содержанию, в частности соответствие действительным характеристикам указанных отправителя, времени отправления и содержания. Обеспечение подлинности информации, реализуемое на основе аутентификации, состоит в достоверном установлении отправителя, а также защите информации от изменения при ее передаче от отправителя к получателю. Своевременно обнаруженное нарушение подлинности и целостности полученного сообщения позволяет предотвратить отрицательные последствия, связанные с дальнейшим использованием такого искаженного сообщения.
Большинство средств защиты информации базируется на использовании криптографических шифров и процедур шифрования/расшифрования. Для защиты информации наряду с криптографией, может использоваться стеганография.
Стеганография, как и криптография, возникла в глубокой древности, но ее расцвет наступил вместе с появлением современных информационных технологий. Методы стеганографии предназначены для передачи сообщений таким образом, что сам факт передачи информации остается скрыт от наблюдателей. Например, в открыто передаваемую цифровую фотографию может быть «спрятано» несколько килобайт текста, который извлекается получателем при помощи специальных алгоритмов. Важно то, что при этом человек не замечает каких-либо искажений в фотографии, содержащей спрятанный текст. В настоящее время методы стеганографии нашли самое широкое применение в системах защиты авторских прав: владельцы цифровых фильмов, фотографий, музыкальных произведений и других данных встраивают туда скрытые метки, что позволяет по «пиратской» копии определить нарушителя авторских прав.
Например, программа Masker шифрует Ваши секретные файлы и прячет их в файлах-носителях. Скачать дистрибутив оценочной версии программы Masker 7.5 можно с сайта разработчика http://www.softpuls.com/ru/masker/
В программе Masker 7.5 для защиты любых объёмов данных используется стеганография — скрытие зашифрованных данных во внешне безобидных файлах-носителях: графических (bmp, gif, jpg, tif), музыкальных (wav, mid, snd, mp3), видео (avi, mov, mpg).
 При этом файлы-носители, в которых прячутся зашифрованные сведения, остаются полностью функциональны. Например, картинка, в которой спрятаны конфиденциальные сведения, при просмотре будет ничем не отличаться от такой же, но без внедренных в нее зашифрованных данных, разве что размером — она будет побольше. Зашифрованные таким способом данные можно не только хранить на своем компьютере, но и пересылать в виде приложения к письму — даже в случае его перехвата в нем будет обнаружена всего-навсего, к примеру, картинка с красивым пейзажем.
При этом файлы-носители, в которых прячутся зашифрованные сведения, остаются полностью функциональны. Например, картинка, в которой спрятаны конфиденциальные сведения, при просмотре будет ничем не отличаться от такой же, но без внедренных в нее зашифрованных данных, разве что размером — она будет побольше. Зашифрованные таким способом данные можно не только хранить на своем компьютере, но и пересылать в виде приложения к письму — даже в случае его перехвата в нем будет обнаружена всего-навсего, к примеру, картинка с красивым пейзажем.
Основные возможности Masker 7.5:
- Прячет любые файлы и целые папки
- Раскрывает файлы-носители и извлекает спрятанные файлы
- Шифрует и сжимает спрятанные файлы
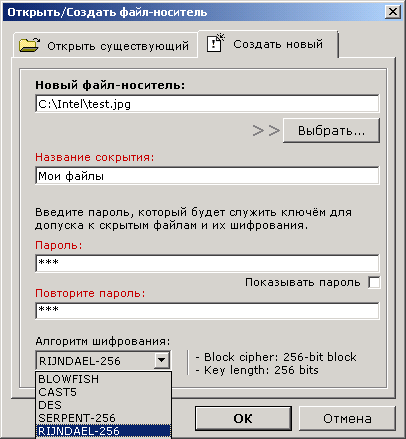
- Поддерживает 7 сильных криптографических алгоритмов (BLOWFISH, RIJNDAEL, etc.)
- Поддержка несколько скрытий в одном файле-носителе
- Функция просмотра
- Функция поиска
- Защита программы от посторонних пользователей
Таким образом, стеганография – это наука о скрытой передаче информации путём сохранения в тайне самого факта её передачи. В отличие от другого направления защиты информации, криптографии, которая скрывает содержимое секретного сообщения, стеганография скрывает само его существование.
Стеганография и криптография не заменяют, а дополняют друг друга. Если файл защищается методами стеганографии, это снижает вероятность обнаружения наличия встроенной в изображение информации. А если эта информация зашифрована (криптография), то она получает ещё один, дополнительный уровень защиты.
Мы начинаем изложение основ криптографии с классической задачи передачи секретных сообщений от некоторого отправителя A к получателю B.
Отправитель сообщений и их получатель могут быть физическими лицами, организациями, какими-либо техническими системами. Иногда об A и B говорят, как об абонентах некоторой сети, о пользователях некоторой компьютерной системы или, еще более формально, как об абстрактных «сторонах» (англоязычный термин «party») или «сущностях» (entity), участвующих в информационном взаимодействии. Но чаще бывает удобно отождествлять участников обмена с некоторыми людьми и заменить формальные обозначения A и B на Алиса и Боб.
Предполагается, что сообщения передаются по так называемому «открытому» каналу связи, в принципе доступному для прослушивания некоторым другим лицам, отличным от получателя и отправителя. Такая ситуация возникает при радиопередаче сообщений (например, посредством мобильного телефона) и возможна при использовании даже таких «проверенных» каналов связи, как проволочный телефон, телеграф, да и обычная почта. Особый интерес как средство передачи данных, стремительно завоевывающее лидирующие позиции во всем мире и в то же время чрезвычайно уязвимое с точки зрения возможности несанкционированного доступа третьих лиц, представляет Интернет. В этой среде легко реализуется не только копирование, но и подмена передаваемых сообщений.
В криптографии обычно предполагается, что у лица, передающего сообщения и (или) их принимающего, есть некоторый противник E, который может быть конкурентом в бизнесе, членом преступной группировки, представителем иностранной разведки или даже чрезмерно ревнивой женой, и этот противник может перехватывать сообщения, передаваемые по открытому каналу, и анализировать их. Часто удобно рассматривать противника как некую особу по имени Ева, которая имеет в своем распоряжении мощную вычислительную технику и владеет методами криптоанализа. Естественно, Алиса и Боб хотят, чтобы их сообщения были непонятны Еве, и используют для этого специальные шифры.
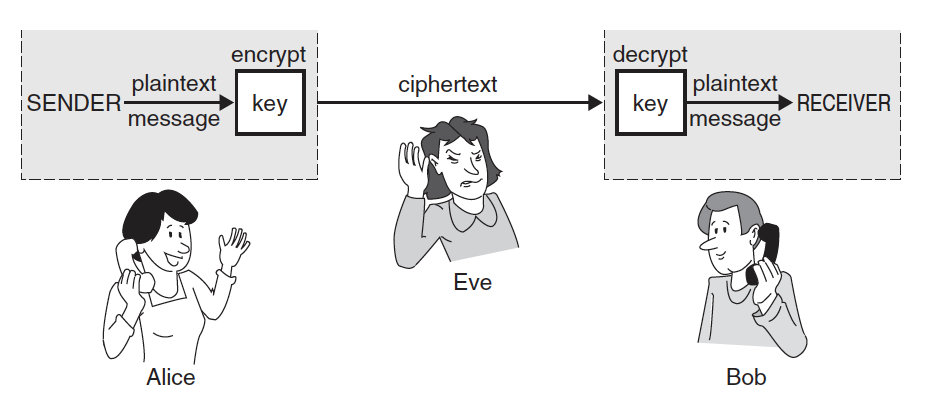
Перед тем как передать сообщение по открытому каналу связи от A к B, A шифрует сообщение, а B, приняв зашифрованное сообщение, дешифрует его, восстанавливая исходный текст. Важно то, что в рассматриваемой нами в этой главе задаче Алиса и Боб могут договариваться об используемом ими шифре (или, скорее, о некоторых его параметрах) не по открытому каналу, а по специальному «закрытому» каналу, недоступному для прослушивания противником. Такой «закрытый канал» может быть организован при помощи курьеров, или же Алиса и Боб могут обмениваться шифрами во время личной встречи и т.п. При этом надо учитывать, что обычно организация такого закрытого канала и передача по нему сообщений слишком дороги по сравнению с открытым каналом и (или) закрытый канал не может быть использован в любое время. Например, курьерская почта намного дороже обычной, передача сообщений с ее помощью происходит намного медленнее, чем, скажем, по телеграфу, да и использовать ее можно не в любое время суток и не в любой ситуации.
Чтобы быть более конкретными, рассмотрим пример шифра. Так как проблема шифрования сообщений возникла еще в глубокой древности, некоторые шифры связаны с именами известных исторических личностей и в качестве первых примеров обычно используют именно такие шифры. Мы также будем придерживаться этой традиции. Начнем с известного шифра Гая Юлия Цезаря, адаптировав его к русскому языку. В этом шифре каждая буква сообщения заменяется на другую, номер которой в алфавите на три больше. Например, А заменяется на Г, Б на Д и т.д. Три последние буквы русского алфавита — Э, Ю, Я — шифруются буквами А, Б, В соответственно. Например, слово ПЕРЕМЕНА после применения к нему шифра Цезаря превращается в ТИУИПИРГ (если исключить букву 13 и считать, что в алфавите 32 буквы).
Последующие римские цезари модифицировали шифр, используя смещение в алфавите на четыре, пять и более букв. Мы можем описать их шифр в общем виде, если пронумеруем (закодируем) буквы русского алфавита числами от 0 до 31 (исключив букву 13).
Таблица 1. Кодирование букв алфавита числами от 0 до 31.
| 0 | 1 | 2 | 3 | 4 | 5 | |
| А а | Б б | В в | Г г | Д д | Е е | |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Ж ж | З з | И и | Й й | К к | Л л | М м |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Н н | О о | П п | Р р | С с | Т т | У у |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| Ф ф | Х х | Ц ц | Ч ч | Ш ш | Щ щ | Ъ ъ |
| 27 | 28 | 29 | 30 | 31 | ||
| Ы ы | Ь ь | Э э | Ю ю | Я я |
Тогда правило шифрования запишется следующим образом:
c = (m + k) mod 32, (1)
где m и c — номера букв соответственно сообщения и шифротекста, а k — некоторое целое число, называемое ключом шифра (в рассмотренном выше шифре Цезаря k = 3). (Здесь и в дальнейшем a mod b обозначает остаток от деления целого числа а на целое число b, причем остаток берется из множества {0,1,…, b — 1}. Например, 13 mod 5 = 3.)
Чтобы дешифровать зашифрованный текст, нужно применить «обратный» алгоритм
m = (c — k) mod 32 (2)
Можно представить себе ситуацию, когда источник и получатель сообщений договорились использовать шифр (1), но для того чтобы усложнить задачу противника, решили иногда менять ключ шифра. Для этого Алиса каким-либо образом генерирует число k, передает его Бобу по закрытому каналу связи, и после этого они обмениваются сообщениями, зашифрованными с помощью этого ключа k . Замену ключа можно проводить, например, перед каждым сеансом связи или после передачи фиксированного числа букв (скажем, каждую десятку символов шифровать со своим k) и т.п. В таком случае говорят, что ключ порождается источником ключа. Схема рассмотренной криптосистемы с секретным ключом приведена на рисунке 1, представленном ниже.
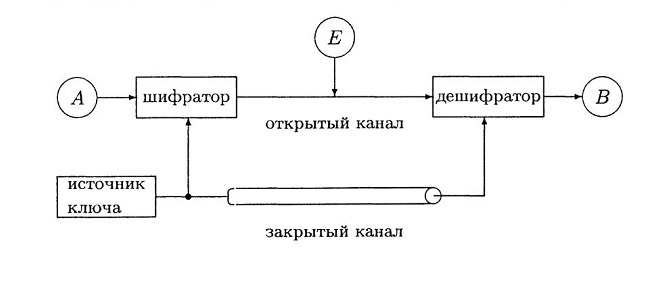
Рис. 1. Классическая система секретной связи
Обратимся теперь к анализу действий противника, пытающегося расшифровать сообщение и узнать секретный ключ, иными словами, вскрыть, или взломать шифр. Каждая попытка вскрытия шифра называется атакой на шифр (или на криптосистему). В криптографии принято считать, что противник может знать использованный алгоритм шифрования, характер передаваемых сообщений и перехваченный шифротекст, но не знает секретный ключ. Это называется «правилом Керкхоффса» в честь ученого, впервые сформулировавшего основные требования к шифрам (A. Kerckhoffs, 1883).

Рис. 2. Огю́ст Керкго́ффс — великий нидерландский криптограф, лингвист, историк, математик. Автор фундаментального труда «Военная криптография», в котором он сформулировал общие требования к криптосистеме, а также утвердил криптоанализ как единственно верный способ испытания шифров.
В нашем примере Ева знает, что шифр был построен в соответствии с (1), что исходное сообщение было на русском языке и что был передан шифротекст ТИУИПИРГ, но ключ Еве не известен.
Наиболее очевидная попытка расшифровки — последовательный перебор всех возможных ключей (это так называемый метод «грубой силы» (brute-force attack)). Итак, Ева перебирает последовательно все возможные ключи к = 1,2, …, подставляя их в алгоритм дешифрования и оценивая получающиеся результаты. Попробуем и мы использовать этот метод. Результаты дешифрования по формуле (2) при различных ключах и шифротексте ТИУИПИРГ сведены в табл. 1.1. В большинстве случаев нам достаточно было расшифровать две-три буквы, чтобы отвергнуть соответствующий ключ (из-за отсутствия слова в русском языке, начинающегося с такого фрагмента).
Таблица 2. Расшифровка слова ТИУИПИРГ путем перебора ключей
| к | m | к | m | к | m | к | m |
| 1 | СЗТ | 9 | ЙЯ | 17 | БЧ | 25 | ЩП |
| 2 | РЖС | 10 | ИЮЙ | 18 | АЦБ | 26 | ШОЩ |
| 3 | ПЕРЕМЕНА | 11 | ЗЭИ | 19 | ЯХА | 27 | ЧН |
| 4 | ОДП | 12 | ЖЬ | 20 | ЮФ | 28 | ЦМ |
| 5 | НГ | 13 | ЕЫ | 21 | ЭУ | 29 | ХЛЦ |
| 6 | МВ | 14 | ДЪ | 22 | Ь | 30 | ФК |
| 7 | ЛБМ | 15 | ГЩ | 23 | Ы | 31 | УЙ |
| 8 | КАЛАЗ | 16 | ВШГ | 24 | Ъ | 32 | ТИУИПИРГ |
Из табл. 2 мы видим, что был использован ключ к = 3 и зашифровано сообщение ПЕРЕМЕНА. Причем для того чтобы проверить остальные возможные значения ключа, нам не требовалось дешифровать все восемь букв, а в большинстве случаев после анализа двух-трех букв ключ отвергался (только при к = 8 надо было дешифровать пять букв, зато при к = 22, 23, 24 хватало и одной, т.к. в русском языке нет слов, начинающихся с Ь, Ъ, Ы).
Из этого примера мы видим, что рассмотренный шифр совершенно нестоек: для его вскрытия достаточно проанализировать несколько первых букв сообщения и после этого ключ к однозначно определяется (и, следовательно, однозначно расшифровывается все сообщение).
В чем же причины нестойкости рассмотренного шифра и как можно было бы увеличить его стойкость? Рассмотрим еще один пример. Алиса спрятала важные документы в ячейке камеры хранения, снабженной пятидекадным кодовым замком. Теперь она хотела бы сообщить Бобу комбинацию цифр, открывающую ячейку. Она решила использовать аналог шифра Цезаря, адаптированный к алфавиту, состоящему из десятичных цифр:
c = (m + k) mod 10 (1.3)
Допустим, Алиса послала Бобу шифротекст 26047. Ева пытается расшифровать его, последовательно перебирая все возможные ключи. Результаты ее попыток сведены в табл. 3.
Таблица 3. Расшифровка сообщения 26047 путем перебора ключей
| к | m | к | m |
| 1 | 15936 | 6 | 60481 |
| 2 | 04825 | 7 | 59370 |
| 3 | 93714 | 8 | 48269 |
| 4 | 82603 | 9 | 37158 |
| 5 | 71592 | 0 | 26047 |
Мы видим, что все полученные варианты равнозначны и Ева не может понять, какая именно комбинация истинна. Анализируя шифротекст, она не может найти значения секретного ключа. Конечно, до перехвата сообщения у Евы было 105 возможных значений кодовой комбинации, а после — только 10. Однако важно отметить то, что в данном случае всего 10 значений ключа. Поэтому при таком ключе (одна десятичная цифра) Алиса и Боб и не могли рассчитывать на большую секретность.
В первом примере сообщение — текст на русском языке, поэтому оно подчиняется многочисленным правилам, различные буквы и их сочетания имеют различные вероятности и, в частности, многие наборы букв вообще запрещены. (Это свойство называется избыточностью текста). Поэтому-то и удалось легко подобрать ключ и расшифровать сообщение, т.е. избыточность позволила «взломать» шифр. В противоположность этому, во втором примере все комбинации цифр допустимы. «Язык» кодового замка не содержит избыточности. Поэтому даже простой шифр, примененный к сообщениям этого языка, становится невскрываемым.
Криптография является методологической основой современных систем обеспечения безопасности информации в компьютерных системах и сетях. Исторически криптография (в переводе с греческого этот термин означает «тайнопись») зародилась как способ скрытой передачи сообщений. Криптография представляет собой совокупность методов преобразования данных, направленных на то, чтобы защитить эти данные, сделав их бесполезными для незаконных пользователей. Такие преобразования обеспечивают решение трех важных проблем защиты данных: обеспечение конфиденциальности, целостности и подлинности передаваемых или сохраняемых данных.
Вопрос 1. Основные понятия криптографической защиты информации
Для обеспечения безопасности данных необходимо поддерживать три основные функции:
- защиту конфиденциальности передаваемых или хранимых в памяти данных;
- подтверждение целостности и подлинности данных;
- аутентификацию абонентов при входе в систему и при установлении соединения.
Для реализации указанных функций используются криптографические технологии шифрования, цифровой подписи и аутентификации.
Конфиденциальность обеспечивается с помощью алгоритмов и методов симметричного и асимметричного шифрования, а также путем взаимной аутентификации абонентов на основе многоразовых и одноразовых паролей, цифровых сертификатов, смарт-карт и т. п.
Целостность и подлинность передаваемых данных обычно достигается с помощью различных вариантов технологии электронной подписи, основанных на односторонних функциях и асимметричных методах шифрования.
Аутентификация разрешает устанавливать соединения только между легальными пользователями и предотвращает доступ к средствам сети нежелательных лиц. Абонентам, доказавшим свою легитимность (аутентичность), предоставляются разрешенные виды сетевого обслуживания.
Основой большинства криптографических средств защиты информации является шифрование данных.
Под шифром понимают совокупность процедур и правил криптографических преобразований, используемых для зашифровывания и расшифровывания информации по ключу шифрования.
Под зашифрованием информации понимается процесс преобразования открытой информации (исходного текста) в зашифрованный текст (шифртекст). Процесс восстановления исходного текста по криптограмме с использованием ключа шифрования называют расшифровыванием (дешифрованием).
Обобщенная схема криптосистемы шифрования показана на рис. 3. Исходный текст передаваемого сообщения (или хранимой информации) М зашифровывается с помощью криптографического преобразования Ek1 с получением в результате шифртекста С:
C = Ek1 (M), где k1 – параметр функции Е, называемый ключом шифрования.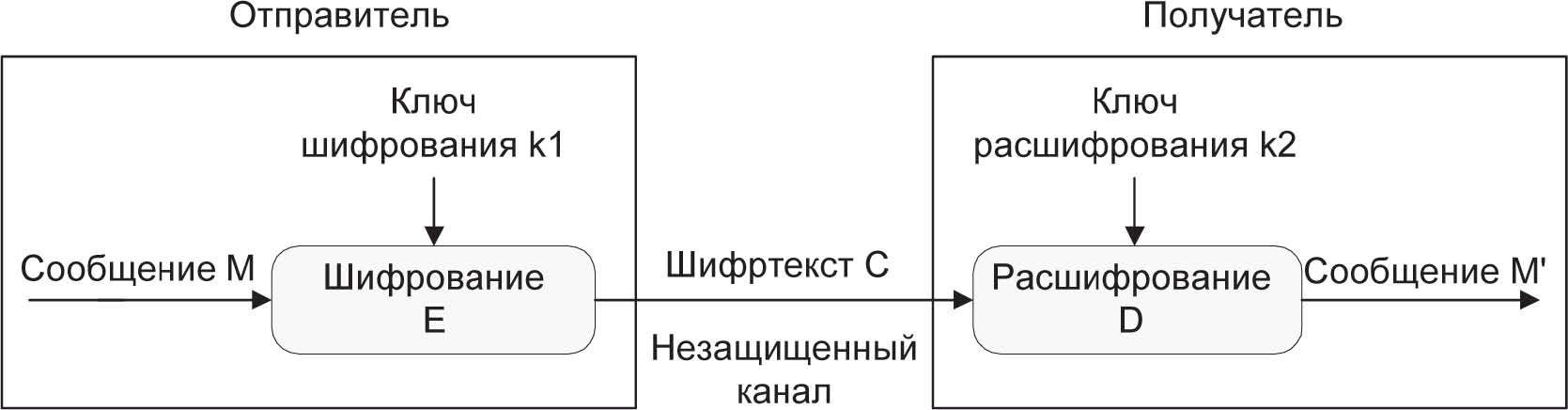
Рис. 3. Обобщенная схема криптосистемы шифрования
Шифртекст С, называемый еще криптограммой, содержит исходную информацию М в полном объеме, однако последовательность знаков в нем внешне представляется случайной и не позволяет восстановить исходную информацию без знания ключа шифрования k1.
Ключ шифрования является тем элементом, с помощью которого можно варьировать результат криптографического преобразования. Данный элемент может принадлежать конкретному пользователю или группе пользователей и являться для них уникальным. Зашифрованная с использованием конкретного ключа информация может быть расшифрована только его владельцем (или владельцами).
Обратное преобразование информации выглядит следующим образом:
M’ = Dk2(C).
Функция D является обратной к функции Е и производит расшифрование шифртекста. Она также имеет дополнительный параметр в виде ключа k2. Ключ расшифрования k2 должен однозначно соответствовать ключу k1, в этом случае полученное в результате расшифрования сообщение М’ будет эквивалентно М. При отсутствии верного ключа k2 получить исходное сообщение М’ = М с помощью функции D невозможно.
Преобразование шифрования может быть симметричным или асимметричным относительно преобразования расшифрования. Соответственно, различают два основных класса криптосистем:
- симметричные криптосистемы;
- асимметричные криптосистемы.
Симметричные криптосистемы (также симметричное шифрование, симметричные шифры) (англ. symmetric-key algorithm) — способ шифрования, в котором для шифрования и расшифровывания применяется один и тот же криптографический ключ.
То есть k1=k2.
До изобретения схемы асимметричного шифрования единственным существовавшим способом являлось симметричное шифрование. Ключ алгоритма должен сохраняться в секрете обеими сторонами. Алгоритм шифрования выбирается сторонами до начала обмена сообщениями.
Ассимметричные криптосистемы — способ шифрования, в котором для шифрования и расшифровывания применяется разные криптографические ключи.
Асимметричные системы называют также двухключевыми криптографическими системами, или криптосистемами с открытым ключом.
В ассиметричных системах k1≠k2.
Известно несколько классификаций криптографических алгоритмов (КА). Одна из них подразделяет КА в зависимости от числа ключей, применяемых в конкретном алгоритме:
- бесключевые КА – не используют в вычислениях никаких ключей;
- одноключевые КА – работают с одним ключевым параметром (секретным ключом);
двухключевые КА – на различных стадиях работы в них применяются два ключевых параметра: секретный и открытый ключи.
Существуют более детальные классификации, например, показанная на рис. 4.
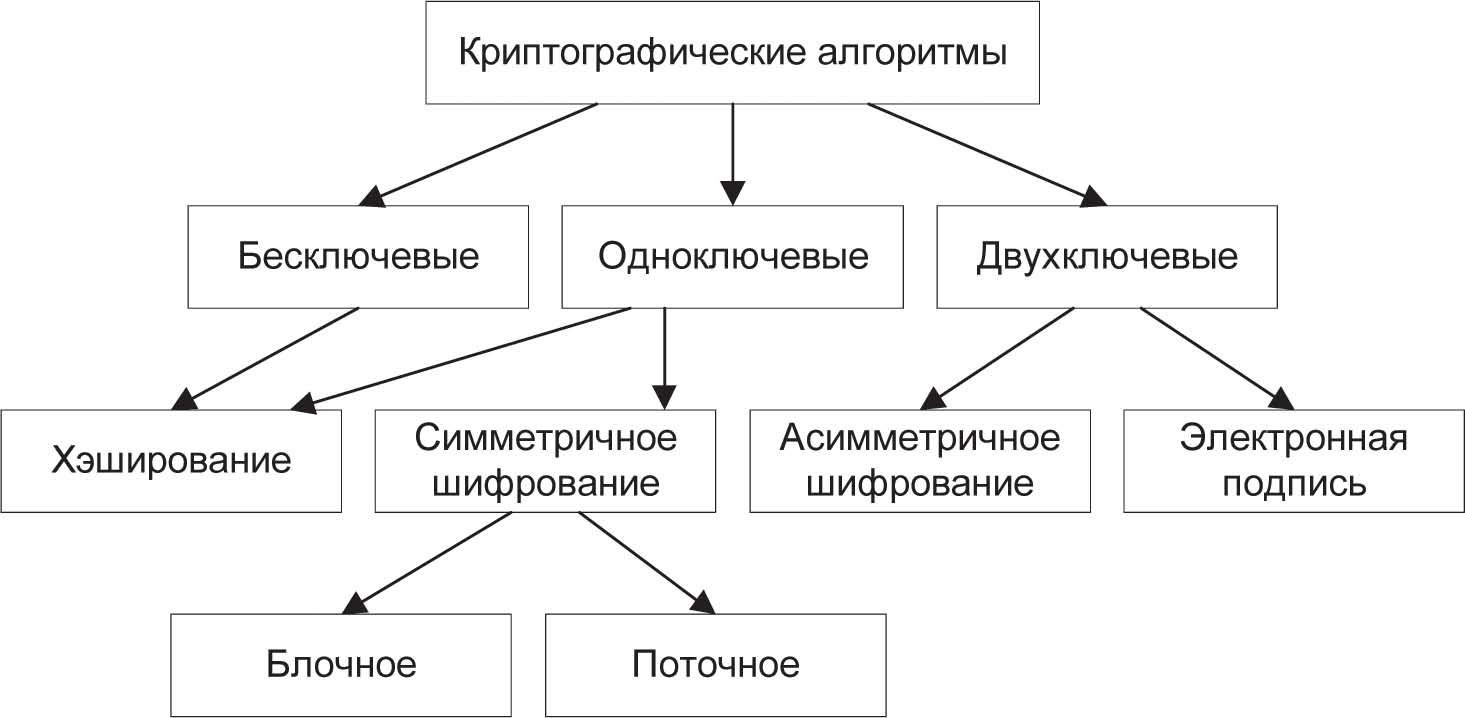
Рис. 4. Классификация криптоалгоритмов защиты информации
Охарактеризуем кратко основные типы КА.
Хэширование – это метод криптозащиты, представляющий собой контрольное преобразование информации: из данных неограниченного размера путем выполнения криптографических преобразований вычисляется хэш-значение фиксированной длины, однозначно соответствующее исходным данным. Хэширование может выполняться как с использованием некоторого секретного ключа, так и без него. Такое криптографическое контрольное суммирование широко используется в различных методах защиты информации, в частности для подтверждения целостности данных, если использование электронной подписи невозможно (например, из-за большой ресурсоемкости) или избыточно. Кроме того, данный метод применяется в схемах электронной подписи («подписывается» обычно хэш-значение данных, а не все данные целиком), а также в схемах аутентификации пользователей (при проверке, действительно ли пользователь является тем, за кого себя выдает).
Симметричное шифрование использует один и тот же ключ как для зашифрования, так и для расшифрования информации. Фактически оба ключа (зашифрования и расшифрования) могут и различаться, но если в каком-либо КА их легко вычислить один из другого в обе стороны, такой алгоритм однозначно относится к симметричному шифрованию.
Симметричное шифрование подразделяется на два вида: блочное и поточное, хотя стоит сразу отметить, что в некоторых классификациях они не разделяются и считается, что поточное шифрование – это шифрование блоков единичной длины.
Блочное шифрование характеризуется тем, что информация предварительно разбивается на блоки фиксированной длины (например, 64 или 128 бит). При этом в различных КА или даже в разных режимах работы одного и того же алгоритма блоки могут шифроваться как независимо друг от друга, так и «со сцеплением» – когда результат шифрования текущего блока данных зависит от значения предыдущего блока или от результата шифрования предыдущего блока.
Поточное шифрование применяется прежде всего тогда, когда информацию невозможно разбить на блоки, – скажем, есть некий поток данных, каждый символ которых требуется зашифровать и отправить, не дожидаясь остальных данных, достаточных для формирования блока. Алгоритмы поточного шифрования шифруют данные побитно или посимвольно.
Асимметричное шифрование характеризуется применением двух типов ключей: открытого – для зашифрования информации – и секретного – для ее расшифрования. Секретный и открытый ключи связаны между собой достаточно сложным соотношением. Главное в этом соотношении – легкость вычисления открытого ключа из секретного и невозможность (за ограниченное время при реальных ресурсах) вычисления секретного ключа из открытого при достаточно большой размерности операндов.
Электронная цифровая подпись (ЭЦП) используется для подтверждения целостности и авторства данных. Как и в случае асимметричного шифрования, в данном методе применяются двухключевые алгоритмы с таким же простым вычислением открытого ключа из секретного и практической невозможностью обратного вычисления. Однако назначение ключей ЭЦП совершенно иное. Секретный ключ применяется для вычисления ЭЦП, открытый ключ необходим для ее проверки. При соблюдении правил безопасного хранения секретного ключа никто, кроме его владельца, не в состоянии вычислить верную ЭЦП какого-либо электронного документа.
Вопрос 2. Симметричные криптосистемы шифрования
Исторически первыми появились симметричные криптографические системы. В симметричной криптосистеме шифрования используется один и тот же ключ для зашифрования и расшифрования информации. Это означает, что любой, кто имеет доступ к ключу шифрования, может расшифровать сообщение. Соответственно, с целью предотвращения несанкционированного раскрытия зашифрованной информации все ключи шифрования в симметричных криптосистемах должны держаться в секрете. Именно поэтому симметричные криптосистемы называют криптосистемами с секретным ключом – ключ шифрования должен быть доступен только тем, кому предназначено сообщение. Симметричные криптосистемы называют еще одноключевыми криптографическими системами, или криптосистемами с закрытым ключом. Схема симметричной криптосистемы шифрования показана на рис. 5.
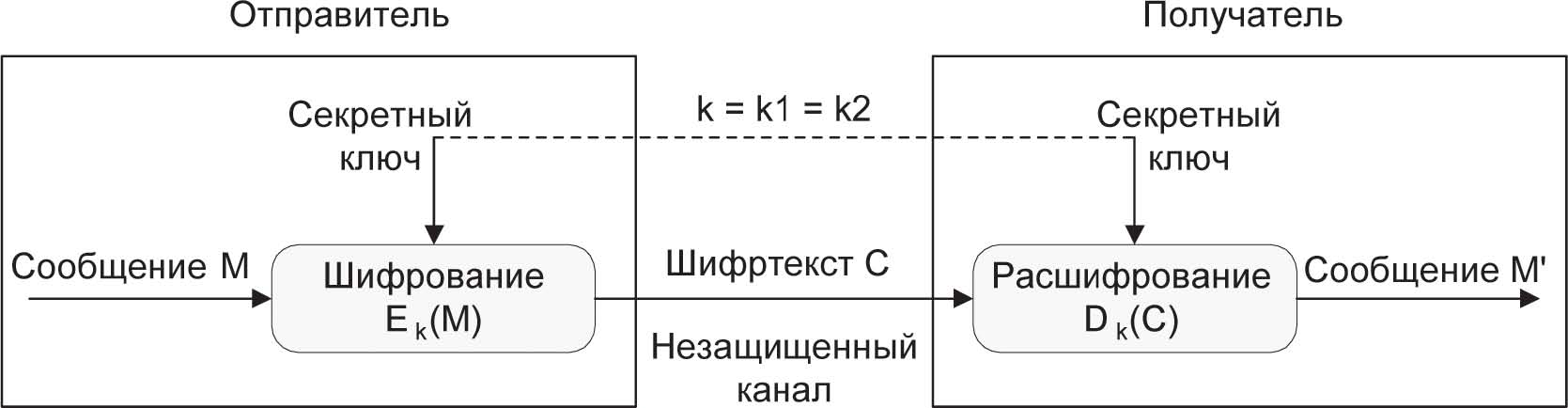
Рис. 5. Схема симметричной криптосистемы шифрования.
Данные криптосистемы характеризуются наиболее высокой скоростью шифрования, и с их помощью обеспечивается как конфиденциальность и подлинность, так и целостность передаваемой информации.
Конфиденциальность передачи информации с помощью симметричной криптосистемы зависит от надежности шифра и обеспечения конфиденциальности ключа шифрования. Обычно ключ шифрования представляет собой файл или массив данных и хранится на персональном ключевом носителе, например, дискете или смарт-карте; обязательно принятие мер, обеспечивающих недоступность персонального ключевого носителя кому-либо, кроме его владельца.
Подлинность обеспечивается за счет того, что без предварительного расшифровывания практически невозможно осуществить смысловую модификацию и подлог криптографически закрытого сообщения. Фальшивое сообщение не может быть правильно зашифровано без знания секретного ключа.
Целостность данных обеспечивается присоединением к передаваемым данным специального кода (имитоприставки), вырабатываемого по секретному ключу. Имитоприставка является разновидностью контрольной суммы, то есть некоторой эталонной характеристикой сообщения, по которой осуществляется проверка целостности последнего. Алгоритм формирования имитоприставки должен обеспечивать ее зависимость по некоторому сложному криптографическому закону от каждого бита сообщения. Проверка целостности сообщения выполняется получателем сообщения путем выработки по секретному ключу имитоприставки, соответствующей полученному сообщению, и ее сравнения с полученным значением имитоприставки. При совпадении делается вывод о том, что информация не была модифицирована на пути от отправителя к получателю.
Симметричное шифрование идеально подходит для шифрования информации «для себя», например, с целью предотвратить несанкционированный доступ к ней в отсутствие владельца. Это может быть, как архивное шифрование выбранных файлов, так и прозрачное (автоматическое) шифрование целых логических или физических дисков.
Обладая высокой скоростью шифрования, одноключевые криптосистемы позволяют решать многие важные задачи защиты информации. Однако автономное использование симметричных криптосистем в компьютерных сетях порождает проблему распределения ключей шифрования между пользователями.
Перед началом обмена зашифрованными данными необходимо обменяться секретными ключами со всеми адресатами. Передача секретного ключа симметричной криптосистемы не может быть осуществлена по общедоступным каналам связи, секретный ключ надо передавать отправителю и получателю по защищенному каналу.
Существуют реализации алгоритмов симметричного шифрования для абонентского шифрования данных – то есть для отправки шифрованной информации абоненту, например, через Интернет. Использование одного ключа для всех абонентов подобной криптографической сети недопустимо по соображениям безопасности. Действительно, в случае компрометации (утери, хищения) ключа под угрозой будет находиться документооборот всех абонентов. В этом случае может быть использована матрица ключей (рис. 6).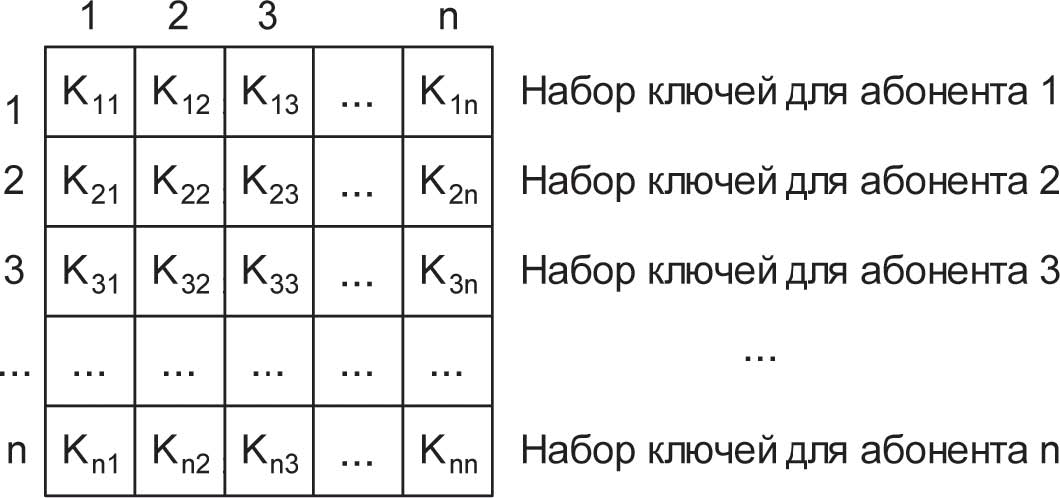
Рис. 6. Матрица ключей
Матрица ключей представляет собой таблицу, содержащую ключи парной связи абонентов. Каждый элемент таблицы Kij предназначен для связи абонентов і и j и доступен только двум данным абонентам. Соответственно, для всех элементов матрицы ключей соблюдается равенство
Kij = Kji.
Каждая і-я строка матрицы представляет собой набор ключей конкретного абонента і для связи с остальными N – 1 абонентами. Наборы ключей (сетевые наборы) распределяются между всеми абонентами криптографической сети. Аналогично сказанному выше сетевые наборы должны распределяться по защищенным каналам связи или из рук в руки.
Характерной особенностью симметричных криптоалгоритмов является то, что в ходе своей работы они производят преобразование блока входной информации фиксированной длины и получают результирующий блок того же объема, но недоступный для прочтения сторонним лицам, не владеющим ключом. Схему работы симметричного блочного шифра можно описать функциями
С = ЕK(М) и M = DK(C),
где М – исходный (открытый) блок данных; С – зашифрованный блок данных.
Ключ K является параметром симметричного блочного криптоалгоритма и представляет собой блок двоичной информации фиксированного размера. Исходный М и зашифрованный C блоки данных также имеют фиксированную разрядность, равную между собой, но необязательно равную длине ключа K.
Блочные шифры являются той основой, на которой реализованы практически все симметричные криптосистемы. Симметричные криптосистемы позволяют кодировать и декодировать файлы произвольной длины. Практически все алгоритмы используют для преобразований определенный набор обратимых математических преобразований.
Методика создания цепочек из зашифрованных блочными алгоритмами байтов позволяет шифровать ими пакеты информации неограниченной длины. Отсутствие статистической корреляции между битами выходного потока блочного шифра используется для вычисления контрольных сумм пакетов данных и в хэшировании паролей. На сегодняшний день разработано достаточно много стойких блочных шифров, например, DES, AES и ГОСТ 28147-89.
Криптоалгоритм считается идеально стойким, если для прочтения зашифрованного блока данных необходим перебор всех возможных ключей до тех пор, пока расшифрованное сообщение не окажется осмысленным. В общем случае стойкость блочного шифра зависит только от длины ключа и возрастает экспоненциально с ее ростом.
К. Шеннон предложил для получения стойких блочных шифров использовать два общих принципа: рассеивание и перемешивание.

Рис. 7. Клод Э́лвуд Ше́ннон (англ. Claude Elwood Shannon; 30 апреля 1916, Петоски, Мичиган, США — 24 февраля 2001, Медфорд, Массачусетс, США) — американский инженер, криптоаналитик и математик. Cчитается «отцом информационного века».
Рассеивание представляет собой распространение влияния одного знака открытого текста на много знаков шифртекста, что позволяет скрыть статистические свойства открытого текста.
Перемешивание предполагает использование таких шифрующих преобразований, которые усложняют восстановление взаимосвязи статистических свойств открытого и шифрованного текстов. Однако шифр должен не только затруднять раскрытие, но и обеспечивать легкость зашифрования и расшифрования при известном пользователю секретном ключе.
Распространенным способом достижения эффектов рассеивания и перемешивания является использование составного шифра, то есть такого, который может быть реализован в виде некоторой последовательности простых шифров, каждый из которых вносит свой вклад в значительное суммарное рассеивание и перемешивание.
В составных шифрах в качестве простых шифров чаще всего используются простые перестановки и подстановки. При перестановке просто перемешивают символы открытого текста, причем конкретный вид перемешивания определяется секретным ключом. При подстановке каждый символ открытого текста заменяют другим символом из того же алфавита, а конкретный вид подстановки также определяется секретным ключом. Следует заметить, что в современном блочном шифре блоки открытого текста и шифртекста представляют собой двоичные последовательности обычно длиной 64 или 128 бит. При длине 64 бит каждый блок может принимать 264 значений. Поэтому подстановки выполняются в очень большом алфавите, содержащем до 264 ≈1019 «символов».
При многократном чередовании простых перестановок и подстановок, управляемых достаточно длинным секретным ключом, можно получить стойкий шифр с хорошим рассеиванием и перемешиванием.
Все действия, производимые блочным криптоалгоритмом над данными, основаны на том факте, что преобразуемый блок может быть представлен в виде целого неотрицательного числа из диапазона, соответствующего его разрядности. Например, 32-битный блок данных можно интерпретировать как число из диапазона 0…4 294 967 295.
Кроме того, блок, разрядность которого представляет собой «степень двойки», можно трактовать как сцепление нескольких независимых неотрицательных чисел из меньшего диапазона (указанный выше 32-битный блок можно также представить в виде сцепления двух независимых 16-битных чисел из диапазона 0…65 535 или в виде сцепления четырех независимых 8-битных чисел из диапазона 0…255).
Над этими числами блочный криптоалгоритм производит по определенной схеме действия, перечисленные в табл. 4.
Таблица 4. Действия, выполняемые криптоалгоритмом над числами
| Действие | Функция |
| Математические функции | |
| Сложение | X = X + V |
| Исключающее ИЛИ | X = X XOR V |
| Умножение по модулю (2N + 1) | X = (X * V ) mod(2N + 1) |
| Умножение по модулю 2N | X = (X * V ) mod(2N ) |
| Битные сдвиги | |
| Арифметический сдвиг влево | X = X SHL V |
| Арифметический сдвиг вправо | X = X SHR V |
| Циклический сдвиг влево | X = X ROL V |
| Циклический сдвиг вправо | X = X ROR V |
| Табличные подстановки | |
| S-box (substitute) | X = Table [X, V ] |
В качестве параметра V для любого из этих преобразований может использоваться:
- фиксированное число (например, X = X + 125);
- число, получаемое из ключа (например, X = X + F(K));
- число, получаемое из независимой части блока (например, X2′ = X2 + F(X1)).
Последний вариант используется в схеме, называемой сетью Фейстеля (по имени ее создателя).
Последовательность выполняемых над блоком операций, комбинации перечисленных выше вариантов V и сами функции F и составляют отличительные особенности конкретного симметричного блочного криптоалгоритма.
Характерным признаком блочных алгоритмов является многократное и косвенное использование материала ключа. Это определяется в первую очередь требованием невозможности обратного декодирования в отношении ключа при известных исходном и зашифрованном текстах. Для решения этой задачи в приведенных выше преобразованиях чаще всего используется не само значение ключа или его части, а некоторая, иногда необратимая функция от материала ключа. Более того, в подобных преобразованиях один и тот же блок или элемент ключа используется многократно. Это позволяет при выполнении условия обратимости функции относительно величины X сделать функцию необратимой относительно ключа K.
Вопрос 2. Функции хэширования
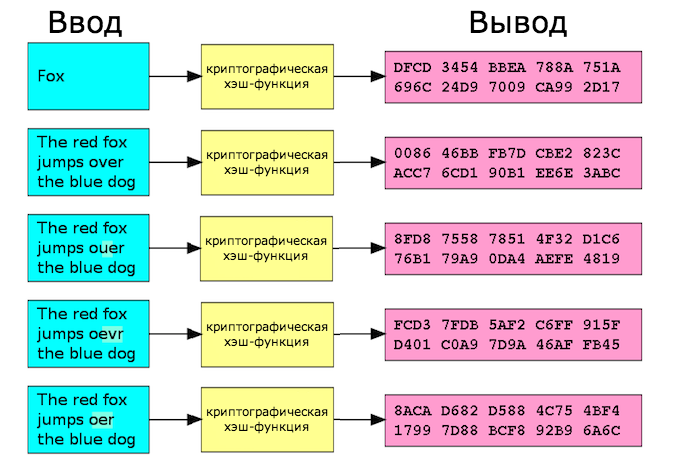
Рис. 8. Пример формирования хэш-функции для разных текстов.
Функция хэширования (хэш-функция) представляет собой преобразование, на вход которого подается сообщение переменной длины M, а выходом является строка фиксированной длины h(M).

Рис. 9. Схема формирования хэша H = h(M)
Иначе говоря, хэш-функция h(·) принимает в качестве аргумента сообщение (документ) M произвольной длины и возвращает хэш-значение (хэш) H = h(M) фиксированной длины (рис. 9).
Хэш-значение h(M) – это дайджест сообщения М, то есть сжатое двоичное представление основного сообщения М произвольной длины. Хэш-значение h(M) формируется функцией хэширования.
Функция хэширования позволяет сжать подписываемый документ M до 128 и более битов (в частности, 128 или 256 бит), тогда как M может быть размером в мегабайт или более. Следует отметить, что значение хэш-функции h(M) зависит сложным образом от документа M и не позволяет восстановить сам документ M.
Функция хэширования должна обладать следующими свойствами:
1. Хэш-функция может быть применена к аргументу любого размера.
2. Выходное значение хэш-функции имеет фиксированный размер.
3. Хэш-функцию h(x) достаточно просто вычислить для любого x. Скорость вычисления хэш-функции должна быть такой, чтобы скорость выработки и проверки ЭЦП при использовании хэш-функции была значительно больше, чем при использовании самого сообщения.
4. Хэш-функция должна быть чувствительна ко всевозможным изменениям в тексте M, таким как вставки, выбросы, перестановки и т. п.
5. Хэш-функция должна быть однонаправленной, то есть обладать свойством необратимости, иными словами, задача подбора документа M’, который обладал бы требуемым значением хэш-функции, должна быть вычислительно неразрешима.
6. Вероятность того, что значения хэш-функций двух различных документов (вне зависимости от их длин) совпадут, должна быть ничтожно мала; то есть для любого фиксированного x с вычислительной точки зрения невозможно найти x’ ≠ x, такое что
h(x’ ) = h(x).
Теоретически возможно, что два различных сообщения могут быть сжаты в одну и ту же свертку (так называемая коллизия, или столкновение). Поэтому для обеспечения стойкости функции хэширования необходимо предусмотреть способ избегать столкновений. Полностью столкновений избежать нельзя, поскольку в общем случае количество возможных сообщений превышает количество возможных выходных значений функции хэширования. Однако вероятность столкновения должна быть низкой.
Свойство 5 эквивалентно тому, что h(. ) является односторонней функцией.
Свойство 6 гарантирует, что не может быть найдено другое сообщение, дающее ту же свертку. Это предотвращает фальсификацию сообщения.
Таким образом, функция хэширования может использоваться для обнаружения изменений сообщения, то есть она может служить для формирования криптографической контрольной суммы (также называемой кодом обнаружения изменений или кодом аутентификации сообщения). В этом качестве хэш-функция используется для контроля целостности сообщения при формировании и проверке электронной цифровой подписи.
Хэш-функции широко используются также для аутентификации пользователей. В ряде технологий информационной безопасности применяется своеобразный прием шифрования – шифрование с помощью односторонней хэш-функции. Своеобразие этого шифрования заключается в том, что оно, по существу, является односторонним, то есть не сопровождается обратной процедурой – расшифрованием на приемной стороне. Обе стороны (отправитель и получатель) используют одну и ту же процедуру одностороннего шифрования на основе хэш-функции. Существует множество криптографических протоколов, основанных на применении хэш-функций.
Широко применяются следующие функции хэширования:
- отечественный стандарт ГОСТ Р34.11–94. Вычисляет хэш размером 256 бит;
- MD (Message Digest – ряд алгоритмов хэширования, наиболее распространенных в мире. Каждый из них вырабатывает 128-битный хэш-код. Алгоритм MD2 – самый медленный из них, MD4 – самый быстрый. Алгоритм MD5 является модификацией MD4, при которой пожертвовали скоростью ради увеличения безопасности. Алгоритм MD5 применяется в последних версиях Microsoft Windows для преобразования пароля пользователя в 16-байтное число;
- SHA-1 (Secure Hash Algorithm Version 1 – алгоритм вычисления дайджеста сообщений, вырабатывающий 160-битный хэшкод входных данных; широко распространен в мире, используется во многих сетевых протоколах защиты информации;
- SHA-2 (Secure Hash Algorithm Version 2) – безопасный алгоритм хэширования версии 2, представляющий собой семейство более стойких хэш-функций SHA-224, SHA-256, SHA384 и SHA-512 с длинами хэша соответственно 224, 256, 384 и 5 12 бит. Следует отметить, что алгоритмы семейства SHA-2 работают в 2–3 раза медленнее популярных хэш-алгоритмов MD5 и SHA-1.
Отечественный стандарт хэширования ГОСТ Р 34.11–94
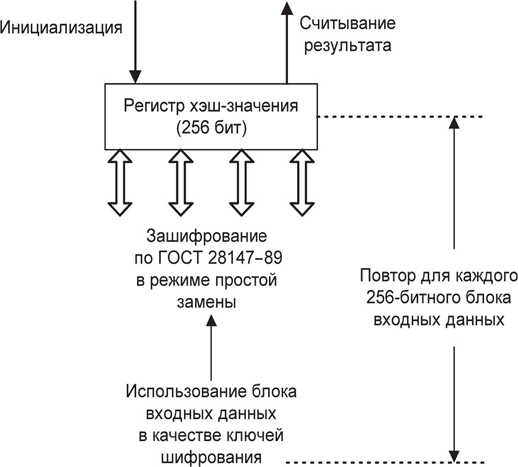
Рис. 10. Хэширование по алгоритму ГОСТ Р 34.11–94
Отечественным стандартом генерирования хэш-функции является алгоритм ГОСТ Р 34.11–94. Этот стандарт является обязательным для применения в качестве алгоритма хэширования в государственных организациях РФ и ряде коммерческих организаций. Коротко данный алгоритм хэширования можно описать следующим образом (рис. 6.20).
Шаг 1. Инициализация регистра хэш-значения. Если длина сообщения не превышает 256 бит – переход к шагу 3, если превышает – переход к шагу 2.
Шаг 2. Итеративное вычисление хэш-значения блоков хэшируемых данных по 256 бит с использованием хранящегося в регистре хэш-значения предыдущего блока. Вычисление включает в себя следующие действия:
- генерацию ключей шифрования на основе блока хэшируемых данных;
- зашифрование хранящегося в регистре хэш-значения в виде четырех блоков по 64 бит по алгоритму ГОСТ 28147–89 в режиме простой замены;
- перемешивание результата.
Вычисление производится до тех пор, пока длина необработанных входных данных не станет меньше или равной 256 бит. В этом случае – переход к шагу 3.
Шаг 3. Дополнение битными нулями необработанной части сообщения до 256 бит. Вычисление хэш-значения аналогично шагу 2. В результате в регистре оказывается искомое хэш-значение.